A nice Cube Simulator which includes the Crazy Cube and much more is pCubes.

To solve the 4x4 Crazy Cube, first solve the circles using the corner sequences (turn slices instead of outer layers), they will remain solved as a 3-Color solution. Solve the rest of the cube normally and then use the following sequences to complete the solution for the circles.

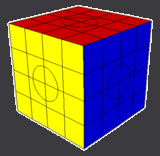
The sequence shown on the first cube below swaps the circles on four faces as shown on the second cube. The second cube is an image not a simulator so it can not be turned, however, all of the configurations on this page are 3-color solutions so the color pairs on opposite faces are the same hence the circle on the (non-visible) left face is blue and the circle on the bottom face is red.

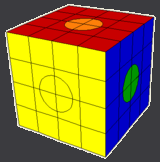This sequences fixes four circles that each have two misplaced quarters as shown on the cube on the right.

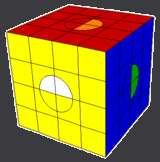
There are two possible configurations with swapped half circles on all six faces, both can be identified by just the three faces shown on the image (this one or the next).

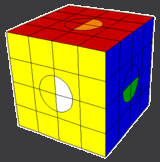
Here is the other possibility for swapped half circles on all six faces. The first four moves fix the circles, the remaining moves fix the two pairs of centers that get swapped by the first four moves.

This sequence fixes swapped half circles on four faces as shown. Moves 6-17 are the 3x3 Supercube sequence (for turning one center on top face) modified such that slices are twisted instead of faces.

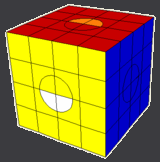The first cube below has swapped half-circles in the same position on four faces and can be converted into the above configuration by doing the first sequence on this page. The second cube below can be converted into the above configuration by doing the second sequence on this page. The mirror-image of the second cube can also be converted to above config by either doing the first sequence (to mirror it) before doing the second sequence or doing the mirror-image of the second sequence.

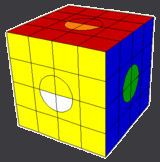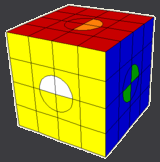The following configuration has four swapped half circles in the same position on four faces. To solve, first apply the modified Supercube sequence to fix the circles and then solve the centers that get misplaced.
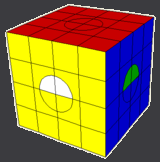